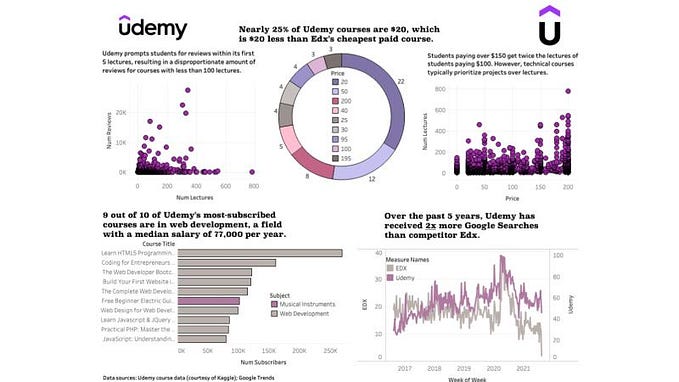
Exploratory Data Analysis on Palmer Archipelago (Antarctica) Penguin Data

Dataset:
The dataset was originally collected and made available by Dr. Kristen Gorman and the Palmer Station, Antarctica LTER. The set contains 344 rows and 7 columns. The 7 attributes are species, culmen length in mm, culmen depth in mm, flipper length in mm, body mass in g, island, and sex.

The data is pretty straightforward. To give a first look at the data, I put its first five rows below. Notice that the data set has missing values “NAN” on the fourth row.

Data Wrangling:
Before we dive into data analysis, we have to do some data wrangling in order to deal with the missing values.
Let’s first check how many missing values we have in total in this dataset.

Based on the picture above, we can see that out of 7 columns, 5 columns have missing data.
The sex column has the most number of missing values.
I decided to use sklearn.impute.SimpleImputer to replace missing data. I chose my imputation strategy as “most frequent” because this strategy can deal with both numeric data and strings. Specifically, the “most frequent” strategy replaces missing data by using the most frequent value along each column. After replacing all the missing data, a transformed version of all rows in our dataset is returned.

Finally, let’s check to see if any missing data remains.

Now, we are good to go for visual data analysis!
Visual Data Analysis:
In this part, I’m going to investigate three major questions regarding this dataset.
Guiding Questions:
- For every species of penguin, is there any correlation between its culmen depth and its culmen length? What about if we combine the species? Will Simpson’s Paradox occur?
- Are there any flipper length differences over islands? Or over species? Can we conclude that either island or species is a confounding variable?
- Do body mass and flipper length differ for different sex on average? If so, by how much? For both sexes, does body mass have any correlation with flipper length?
Question 1: Culmen Depth v.s Culmen Length for Species:
First, Let’s see how many penguins we have for each species.

There’re 152 Adelie penguins, 124 Gentoo penguins, and 68 Chinstrap penguins.
Notice that the sample sizes vary a lot for different species. In order to avoid any over or under-sampling problem, I adopted simple random sampling for each species to balance the data set.
I randomly chose 50 penguins from each species. If you use the same seed number 234, you can get the same result as me.

After balancing the dataset, I drew a scatter plot between culmen depth and culmen length for each species, and I also fit a best-fitting line for each scatterplot.

From the graph above, we can see that, for all three species, there exists a relatively weak positive correlation between culmen depth and culmen length. The correlation is stronger for Chinstrap and Gentoo but especially weak for Adelie.
Now, Let’s calculate the exact correlations between culmen depth and culmen length for three species:

We get the correlation for Adelie is 0.285 (a weak positive correlation), for Chinstrap is 0.622 (a moderate positive correlation), and for Gentoo is 0.49 (a moderate positive correlation).
Thus, we can conclude a weak positive correlation exists between culmen depth and culmen length for Adelie, Chinstrap, and Gentoo.
But what about if we combine the species? Does this weak positive correlation remain?
Let’s combine these three samples into a new data set named “df_species.”

Draw a scatter plot between culmen depth and culmen length for df_species and fit a best-fitting line for the scatterplot.

The result is very unexpected. Instead of having a weak positive correlation, we get a weak negative correlation between culmen depth and culmen length after combining the species.
We can also calculate the exact correlation. It turns out to be -0.089.

This surprising result is actually what statisticians called Simpson’s Paradox. Simpson’s Paradox occurs when “a trend appears in several different groups of data but disappears or reverses when these groups are combined.” We have to be especially careful with Simpson’s Paradox because this will often lead to misleading results.
Question 2: flipper length over islands and over species
Similarly, let’s first see how many penguins we have on each island!

There’re 168 penguins on Biscoe Island, 124 on Dream Island, and 52 on Torgersen Island.
For the same reason in Question 1, I did simple random sampling for each island to balance the data set. I randomly chose 50 penguins from each island and combined them into a new dataset named df_island.

After balancing the data set, I drew a boxplot for flipper length over each island.

From the graph above, we see that penguins on Biscoe island have a large flipper length on average than penguins on Dream island and Torgersen island.
Let’s continue to draw a boxplot for flipper length over species to investigate whether there’s any difference over species.

From the graph above, we can see that Gentoo penguins have a much larger flipper length than Adelie penguins and Chinstrap penguins on average.
At this point, we naturally come up with this concern: Does Biscoe Island’s larger average flipper length come from the fact that most penguins who live on Biscoe island are Gentoo?
To understand this question, let’s first do some statistics to see how different species of penguins are distributed over islands.

From the picture above, we get the result that Biscoe island is the only island with Gentoo penguins living on it in our df_island sample. However, since there’s no causal relationship established, we can only infer that flipper length differences over islands may come from the fact that there’re differences over species, and certain species tend to live on certain islands. We need to conduct controlled experiments to conclude that island is indeed a confounding variable.
Question 3: Body Mass and Flipper Length over Sex:
Again, Let’s see how many penguins we have for each sex.

There’re 168 male penguins and 165 female penguins.
Do simple random sampling to choose 100 penguins from each sex randomly.
Let’s draw a histogram of body mass for both sexes.

From the graph, we can see that overall, male penguins have bigger body masses than female penguins.
We can specifically calculate the average body mass for males and females to compare the difference.

The average body mass of males is 759.5 grams larger than the average body mass of females.
Similarly, we draw a histogram of flipper length for both sexes.

Again, overall, male penguins have larger flipper lengths than female penguins.

The average flipper length of males is 7.78 mm longer than the average flipper length of females.
Since a male penguin has both a larger body mass and a longer flipper length, is there any correlation between body mass and flipper length for male penguins? what about female penguins?
I drew a scatter plot between body mass and flipper length for both sexes, and fit a best-fitting line for each scatterplot.

It turns out that there is a strong positive correlation between body mass and flipper length for both males and females.
Let’s calculate the specific correlations between body mass and flipper length for each sex.

We get the correlation for males is 0.863 and for females is 0.872. Both correlations are over 0.8, which means they are very strong correlations.
Summary:
Finally, to reiterate my findings for my three guiding questions:
- There exists a weak positive correlation between culmen depth and culmen length for each species. However, after combing these three species, Simpson’s Paradox occurs, and a weak negative correlation between culmen depth and culmen length appears.
- Penguins on Biscoe island have a large flipper length on average, and Gentoo penguins have a larger flipper length on average. Since Biscoe island is the only island with Gentoo penguins living on it, we can possibly infer that flipper length differences over islands may come from the fact that there’re differences over species, and certain species tend to live on certain islands. However, without controlled experiments, we can not conclude that island is a confounding variable.
- Male penguins tend to have larger body masses and longer flipper lengths than female penguins. For both males and females, there exists a strong positive correlation between body mass and flipper length.